Quadrilaterals ⇒⇒ Exercise 8.2

Question 1

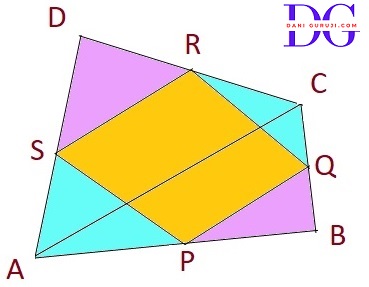
ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA. AC is a diagonal. Show that :

(i) SR || AC and SR = 1/2 AC
(ii) PQ = SR
(iii) PQRS is a parallelogram

Solution :

Let's start with a parallelogram, ABCD ,

where P, Q, R and S are the mid points of the sides AB, BC, CD and DA. And It has one diagonal, AC .

(i) SR || AC and SR = 1/2 AC

Consider △DAC :

The points S and R are the mid-points of the sides DA and DC, respectively.

( By the Mid-point Theorem, the line segment connecting the midpoints of two sides of a triangle is parallel to the third side and is half the length of the third side.)

⇒ SR || AC

⇒ SR = 1/2 AC.

(ii) PQ = SR

Consider △ABC :

P and Q are the mid-points of sides AB and BC, respectively.

( By the Mid-point Theorem,)

⇒ PQ || AC

⇒ PQ = 1/2 AC.

From part (i), we established that SR = 1/2 AC

Since both PQ and SR are equal to half the length of AC, it follows that

⇒ PQ = SR

Hence, proved that PQ = SR.

(iii) PQRS is a parallelogram

A quadrilateral is a parallelogram if one pair of opposite sides is both parallel and equal in length.

From part (ii), we know that

⇒ PQ = SR

From parts (i) and (ii), we have SR || AC and PQ || AC.

Since both SR and PQ are parallel to the same line segment AC, they must be parallel to each other. Thus, PQ || SR.

Because the quadrilateral PQRS has one pair of opposite sides (PQ and SR) that are both parallel and equal, PQRS is a parallelogram.

Question 2

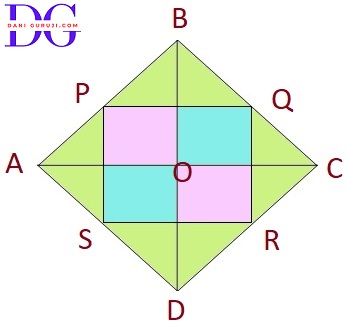
ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.

Solution :

Let's start with a rhombus, ABCD ,

where P, Q, R and S are the mid points of the sides AB, BC, CD and DA. Join AC and BD.

PQRS is a Rectangle Parallelogram

Consider △ABC :

P and Q are the mid-points of sides AB and BC, respectively.

( By the Mid-point Theorem, the line segment connecting the midpoints of two sides of a triangle is parallel to the third side and is half the length of the third side.)

⇒ PQ || AC

⇒ PQ = 1/2 AC..

Consider △ADC :

S and R are the mid-points of sides AD and CD, respectively.

( By the Mid-point Theorem,)

⇒ SR || AC

⇒ SR = 1/2 AC.

From these two statements, we get PQ || SR and PQ = SR

Because the quadrilateral PQRS has one pair of opposite sides (PQ and SR) that are both parallel and equal, PQRS is a parallelogram.

Now, we prove that one of the angles in the parallelogram PQRS is a right angle.

Consider the other two sides of the parallelogram, QR and PS.

Now, Consider △ABD :

P and S are the mid-points of sides AB and AD, respectively.

( By the Mid-point Theorem,)

⇒ PS || BD

⇒ PS = 1/2 BD..

Now, Consider △BCD :

Q and R are the mid-points of sides BC and CD, respectively.

( By the Mid-point Theorem,)

⇒ QR || BD

⇒ QR = 1/2 BD .

From these two statements, we get PS || QR and PS = QR

( We know from the properties of a rhombus that its diagonals, AC and BD, are perpendicular to each other (AC⊥BD).)

Since PQ is parallel to AC and QR is parallel to BD, and AC is perpendicular to BD, it logically follows that PQ must be perpendicular to QR.

This means that $\angle $PQR=90°.

A parallelogram with a right angle is a rectangle.

Since PQRS is a parallelogram and $\angle $PQR=90°, it must be a rectangle.

Question 3

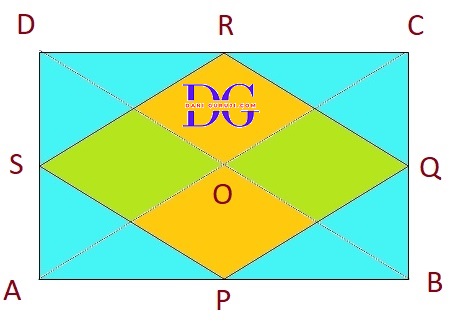
ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.

Solution :

Let's start with a rectangle, ABCD ,

where P, Q, R and S are the mid points of the sides AB, BC, CD and DA. Join AC and BD.

PQRS is a rhombus

Consider △ABC :

P and Q are the mid-points of sides AB and BC, respectively.

( By the Mid-point Theorem, the line segment connecting the midpoints of two sides of a triangle is parallel to the third side and is half the length of the third side.)

⇒ PQ || AC

⇒ PQ = 1/2 AC.

Consider △ADC :

S and R are the mid-points of sides AD and CD, respectively.

( By the Mid-point Theorem,)

⇒ SR || AC

⇒ SR = 1/2 AC.

From these two statements, we get( PQ || SR )and ( PQ = SR ) and = 1/2 AC ----- eq.(i)

Now, Consider △ABD :

P and S are the mid-points of sides AB and AD, respectively.

( By the Mid-point Theorem,)

⇒ PS || BD

⇒ PS = 1/2 BD..

Now, Consider △BCD :

Q and R are the mid-points of sides BC and CD, respectively.

( By the Mid-point Theorem,)

⇒ QR || BD

⇒ QR = 1/2 BD .

From these two statements, we get( PS || QR )and ( PS = QR ) and = 1/2 BD. ----- eq.(ii)

Now, The diagonals of a rectangle are equal in length, so AC = BD.

Now, From eq.(i) and (ii), we have:

PQ = SR = 1/2 AC

PS = QR and = 1/2 BD

Since AC = BD, it follows that all four sides are equal: PQ = SR = PS = QR.

( The diagonals of a rectangle are equal,)

This means, a quadrilateral with four equal sides is a rhombus.

Question 4

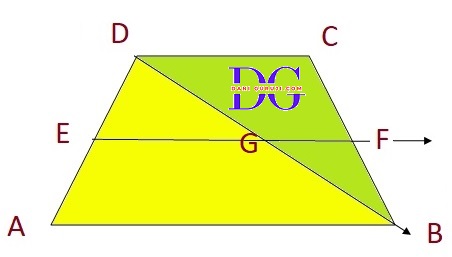
ABCD is a trapezium in which AB || DC,
BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F see Fig. Show that F is the mid-point of BC.

Solution :

ABCD is a trapezium, where AB || DC, E is the mid-point of AD and EF || AB.

Let EF intersect BD at point G.

Consider △DAB :

E is the midpoint of side AD (given).

EG is a line drawn through E parallel to AB,since EF || AB, and G is a point on EF

( According to the Converse of the Midpoint Theorem, the line segment drawn from the midpoint of one side of a triangle and parallel to another side bisects the third side..)

Therefore, G is the midpoint of the side DB.

Now, Consider △BCD

G is the midpoint of the side DB ( proved in step 1)

Proving GF is parallel to DC

We know that EF || AB (given).

We also know that AB || DC (given, ABCD is a trapezium).

Lines parallel to the same line are parallel to each other. So, EF || DC.

Therefore, the segment GF is also parallel to DC.

Therefore, by using converse of mid-point theorem, F is the mid-point of BC.

Question 5

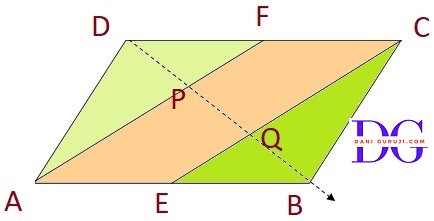
In a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively (see Fig.). Show that the line segments AF and EC trisect the diagonal BD.

Solution :

ABCD is a parallelogram, where E and F are the mid-points of sides AB and CD.

Consider the quadrilateral AECF

ABCD is a parallelogram,

We know that, Opposite sides of a parallelogram are equal and parallel.

So, ∴ AB || CD and AB = CD

E and F are the midpoints of AB and DC, respectively.

Therefore, AE = 1/2 AB and FC = 1/2 CD.

Since, AB = CD , it follows that AE = FC

Also, since AB || DC

∴ AE || FC

A quadrilateral with one pair of opposite sides equal and parallel is a parallelogram.

Thus, AECF is a parallelogram.

Consider △APB :

The quadrilateral AECF is a parallelogram, which means AF || EC

The line segment EQ is a part of EC, so EQ || AF

E is the midpoint of AB (given).

( According to the Converse of the Midpoint Theorem, the line segment drawn from the midpoint of one side of a triangle and parallel to another side bisects the third side.)

Therefore, the line EQ bisects the side PB.

This means that Q is the midpoint of PB, so PQ = QB. ---- equations (1)

Consider △DQC :

The quadrilateral AECF is a parallelogram, which means AF || EC

The line segment FP is a part of AF, so FP || QC

F is the midpoint of DC (given).

( According to the Converse of the Midpoint Theorem, )

Therefore, the line FP bisects the side DQ.

Therefore, P is the midpoint of DQ, so PQ = DP. ------ equations (2)

From equations (1) and (2) we get :

⇒ PQ = QB = DP

Since the line segments AF and EC divide the diagonal BD into three equal parts, they trisect the diagonal BD.

Question 6

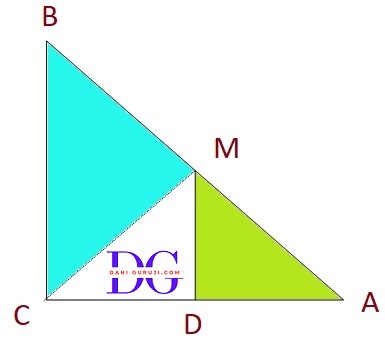
ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that.

(i) D is the mid-point of AC
(ii) MD ⊥ AC
(iii) CM = MA = 1/2 AB

Solution :

(i) D is the mid-point of AC

Given that M is the mid-point of the hypotenuse AB, and the line MD is parallel to BC.

Consider △ABC :

M is the mid-point of AB.

The line segment MD is drawn from M parallel to the side BC

( According to the Converse of the Midpoint Theorem, the line segment drawn from the midpoint of one side of a triangle and parallel to another side bisects the third side.)

Therefore, the line MD bisects AC, which means D is the mid-point of AC.

(ii) MD ⊥ AC

We are given that △ABC is right-angled at C

So $\angle $C = 90°

We are also given that MD || BC

The line AC as a transversal intersecting the parallel lines MD and BC.

$\angle $ADM = $\angle $ACB

( the corresponding angles are equal.)

Since $\angle $ACB = 90°, it follows that $\angle $ADM = 90°.

Therefore, MD ⊥ AC.

(iii) CM = MA = 1/2 AB

M is the midpoint of the hypotenuse AB,

So AM = MB = 1/2 AB

Consider the Δ CDM and Δ ADM:

⇒ DM = DM

( common side)

⇒ AD = CD

( from part i)

⇒ $\angle $CDM = $\angle $ADM

( from part i)

∴ Δ CDM $\cong$ Δ ADM

( by the SAS congruence rule. )

Since the triangles are congruent, their corresponding parts are equal (CPCT).

Therefore, CM = MA

We know that MA = 1/2 AB because M is the midpoint of AB.

From the above proof, we have CM = MA

Combining these two statements, we get CM = MA = = 1/2 AB